Equilibrio de fases para un sistema monocomponente (Continuación)
La energía libre o también conocida como la energía de Gibbs, es una función de estado extensiva con unidades de energía, a presión y temperatura constantes, que da la condición de equilibrio y de espontaneidad para una reacción química. La combinación de variables U + p V — T S aparece con frecuencia y se designa por el símbolo especial G. Por definición.
G = U + p V - T S = H - T S = A + pV.
Si ∆G < 0 proceso espontáneo
∆G > 0 proceso no espontáneo
Si ∆G =0 los procesos directos e inversos tienen la misma tendencia a producirse, por lo que el sistema se encuentra en equilibrio.
Las energías libres molares también reciben el nombre de potenciales químicos µ. El sentido físico del potencial químico es la variación de energía libre del sistema correspondiente a un cambio infinitesimal en el número de moles del constituyente i cuando la presión, temperatura y cantidad de moles de los otros constituyentes se mantienen constantes
µi = Gi
Un sistema está en equilibrio material cuando el potencial químico de cada componente es constante en todos los puntos del sistema
Además de las propiedades mecánicas p y V, un sistema tiene tres propiedades fundamentales: T, U y S, definidas por las leyes de la termodinámica y tres propiedades compuestas H, A y G, que son importantes. El análisis a sistemas que producen sólo trabajo de expansión, queda que dWa = 0. Con esta restricción, la condición de equilibrio:
dU = T dS - p dV
Esta combinación de la primera y segunda leyes de la termodinámica es la ecuación fundamental de la termodinámica. Utilizando las definiciones de las funciones compuestas:
H = U + pV A = V - TS G = U + pV - TS
mediante diferenciación, obtenemos:
dH = dU + p dV + V dp
dA= dU - T dS - S dT
dG = dU + p dV + V dp - T dS - S dT
Reemplazando [dU = T dS - p dV] (1) en cada una de estas ecuaciones:
dH = T dS + V dp (2)
dA = -S dT - p dV (3)
dG = -S dT + V dp (4)
Estas cuatro ecuaciones suelen denominarse Ecuaciones fundamentales de la termodinámica. La ecuación (1) relaciona las variaciones de la energía con variaciones de entropía y volumen. La ecuación (2) relaciona las variaciones de entalpía con las de entropía y presión. La ecuación (3) relaciona las variaciones de la energía de Helmholtz dA con cambios de la temperatura y del volumen. La ecuación (4) relaciona las variaciones de la energía de Gibbs con variaciones de temperatura y presión. Como las expresiones del segundo término de estas ecuaciones son diferenciales exactas, sus derivadas cruzadas serán iguales. De esta manera, se obtienen las cuatro relaciones de Maxwell:
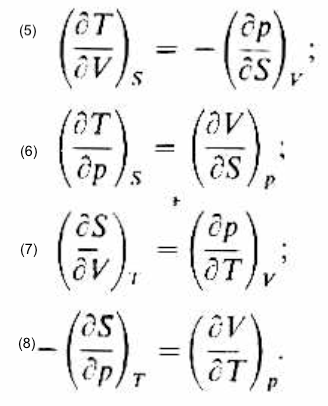
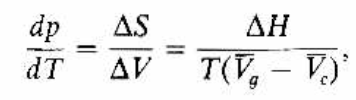
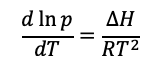
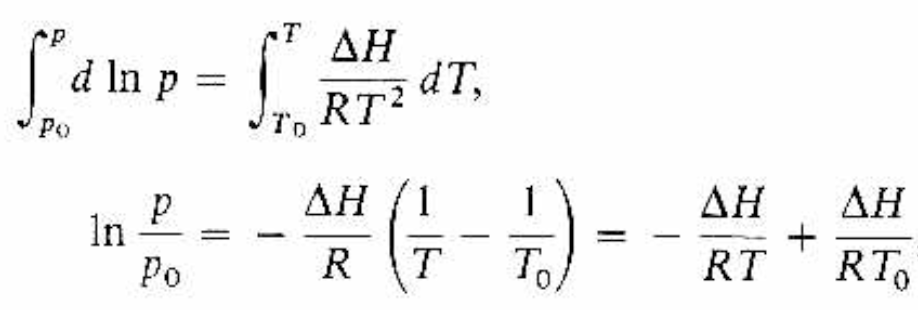
Comentarios
Publicar un comentario